10 - Game AI strategies

AI

First option for AI opponent would be to just use random legal moves. Hey, at least it does something.
Quick thinking shows, that this has a lot of room for improvement - not all moves are equal. In game of checkers - maybe move that ends up with removing opponents piece(s) from board should be ranked higher? Or move that makes your piece into king. So we need some kind of function that allow us evaluate different resulting game states after move and assign some numerical value to it. Typically this function is heuristical function. And usually values range from -1 to 1. -1 might be player A win, and 1 is player B win.

And if we are able try out all the bossible moves one after each other - then we need just values of -1 and 1. And we can draw up path through all the moves that would lead us to our victory (if possible).
This is not possible in most of games.

For example, tic-tac-toe has 9 possible moves in first iteration. Then oponent has 8 moves after that, etc..
So we and up with 9! or fewer possible combos - just 362 880 terminal board positions. Easy to calculate to the end.
There are even books printed with them... (https://www.goodreads.com/en/book/show/18490871-tic-tac-tome)

For chess - its over 10^40 nodes. So we cannot construct the game tree in reality. We will just run out of memory and time.

Game tree

Tree (partial) of Tic-Tac-Toe

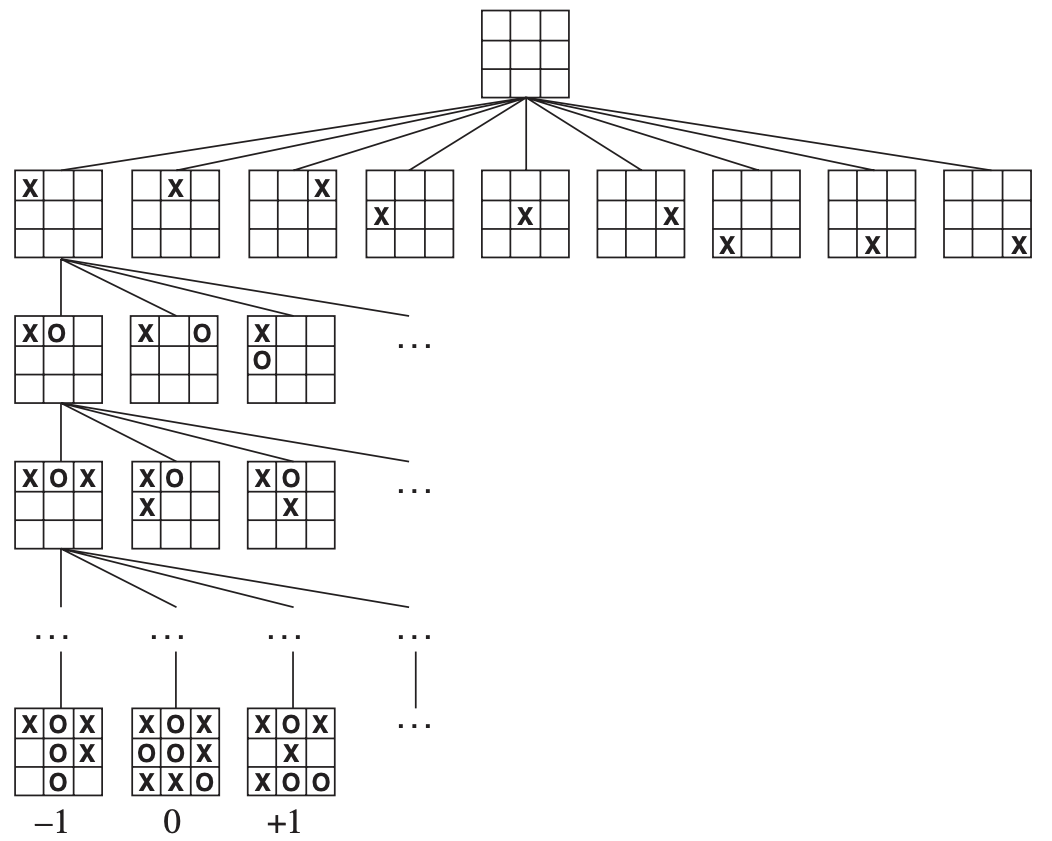
One player tries to go to +1 end state (MAX) and opponent to -1 end state (MIN).

In a normal search problem, the optimal solution would be a sequence of actions leading to a goal state—a terminal state that is a win. In adversarial search, MIN has something to say about it. MAX therefore must find a contingent strategy, which specifies MAX’s move in the initial state, then MAX’s moves in the states resulting from every possible response by MIN, then MAX’s moves in the states resulting from every possible response by MIN to those moves, and so on.

An optimal strategy leads to outcomes at least as good as any other strategy when one is playing an infallible opponent.

Minimax

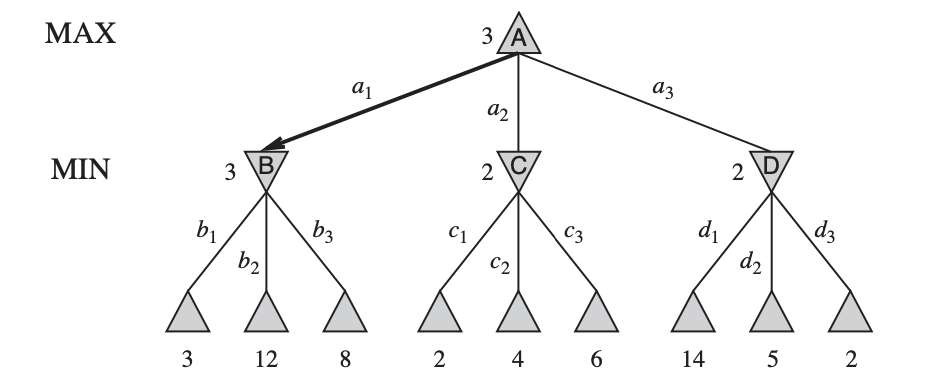
Two move tree... (A - MAX NODES, V - MIN NODES)

Given a game tree, the optimal strategy can be determined from the minimax value of each node, MINIMAX(n). The minimax value of a node is the utility (for MAX) of being in the corresponding state, assuming that both players play optimally from there to the end of the game. Obviously, the minimax value of a terminal state is just its utility function. Furthermore, given a choice, MAX prefers to move to a state of maximum value, whereas MIN prefers a state of minimum value.

This definition of optimal play for MAX assumes that MIN also plays optimally — it maximizes the worst-case outcome for MAX.

Alpha-Beta pruning

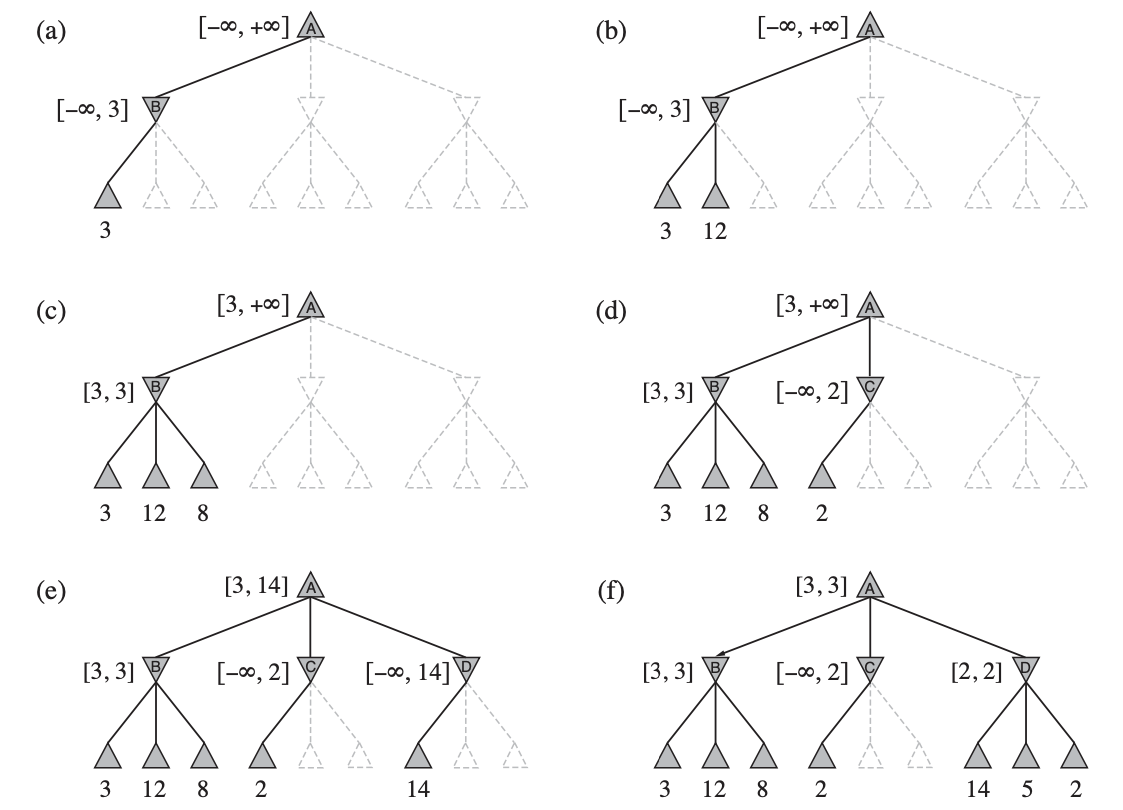
(a) The first leaf below B has the value 3. Hence, B, which is a MIN node, has a value of at most 3. (b) The second leaf below B has a value of 12; MIN would avoid this move, so the value of B is still at most 3. (c) The third leaf below B has a value of 8; we have seen all B’s successor states, so the value of B is exactly 3. Now, we can infer that the value of the root is at least 3, because MAX has a choice worth 3 at the root. (d) The first leaf below C has the value 2. Hence, C, which is a MIN node, has a value of at most 2. But we know that B is worth 3,so MAX would never choose C. Therefore, there is no point in looking at the other successor states of C. This is an example of alpha–beta pruning. (e) The first leaf below D has the value 14, so D is worth at most 14. This is still higher than MAX’s best alternative (i.e., 3), so we need to keep exploring D’s successor states. Notice also that we now have bounds on all of the successors of the root, so the root’s value is also at most 14. (f) The second successor of D is worth 5, so again we need to keep exploring. The third successor is worth 2, so now D is worth exactly 2. MAX’s decision at the root is to move to B, giving a value of 3.

Alpha-Beta pruning algorithm

α = the value of the best (i.e., highest-value) choice we have found so far at any choice point along the path for MAX.
β = the value of the best (i.e., lowest-value) choice we have found so far at any choice point along the path for MIN.

Cutting off search

Apply cut-off at certain depth (and evaluate the board state).

Instead of terminal-test and utility function:

if CUTOFF-TEST(state, depth) then return HEURISTIC(state)

Increment dept on every recursive call. Compare to some max (don't forget also the terminal states).